A good question was brought up by my students in the lab exercise in the course Electronics I yesterday: What actually makes the cut-off frequency of a filter circuit (1st order) so special? Why do we look out for a point which happens to be located ![]() or a factor of
or a factor of ![]() under the amplitude of the pass band? Why not
under the amplitude of the pass band? Why not ![]() ,
, ![]() ,
, ![]() ?
?
The first answer, which has some historical relevance, would be to look at a resistor ![]() and a signal with an amplitude
and a signal with an amplitude ![]() and another signal with an amplitude
and another signal with an amplitude ![]() while calculating the electrical power:
while calculating the electrical power:
[ P_0 = frac{V_0^2}{R}qquad P_1 = frac{V_1^2}{R} = frac{left(V_0,sfrac{1}{sqrt{2}}right)^2}{R} = frac{1}{2},P_0 ]
The power has been reduced to half the original power, it could be the electric power which is converted to sound waves in a speaker, or the power converted to electromagnetic waves in an antenna.
But already here we can make one important observation: ![]()
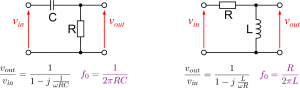
Is this everything then? It still sounds random to choose exactly this point. If we for example look at a simple RC filter then we can show another reason which makes this point’s frequency so special. In a low-pass filter we have a constant amplitude ![]() for low frequencies while we observed mathematically and experimentally that the amplitude drops with
for low frequencies while we observed mathematically and experimentally that the amplitude drops with ![]() per decade of frequency for high frequencies. If we draw out these two asymptotic lines in a Bode diagram, then we will find exactly one point where the lines intersect – you guessed it: it’s at the cut-off frequency (the same holds of course true for a high-pass filter). We can see this if we zoom into the area around the cut-off frequency in a Bode diagram:
per decade of frequency for high frequencies. If we draw out these two asymptotic lines in a Bode diagram, then we will find exactly one point where the lines intersect – you guessed it: it’s at the cut-off frequency (the same holds of course true for a high-pass filter). We can see this if we zoom into the area around the cut-off frequency in a Bode diagram:
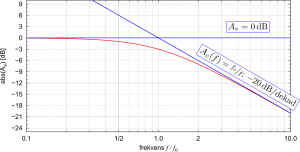
Then was this everything now? Is there more about the cut-off frequency?
As we also saw we have a phase angle of ![]() (high-pass) or
(high-pass) or ![]() (low-pass) between the input- and the output signal at the cut-off frequency. In the complex notation of the
(low-pass) between the input- and the output signal at the cut-off frequency. In the complex notation of the ![]() -method this correlates to the fact that the real and the imaginary part of the transfer function
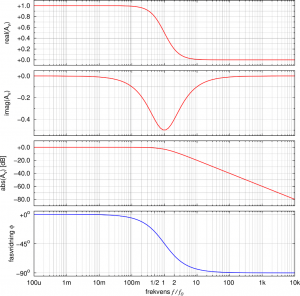
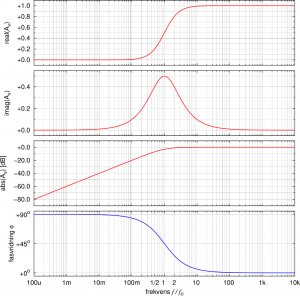
-method this correlates to the fact that the real and the imaginary part of the transfer function ![]() have the same magnitude at this point. The relation between real part, imaginary part, amplitude and phase angle I have plotted below for both the low-pass and the high-pass filter.
have the same magnitude at this point. The relation between real part, imaginary part, amplitude and phase angle I have plotted below for both the low-pass and the high-pass filter.
It is interesting to observe that the imaginary part actually reaches a minimum at this point (![]() for the low-pass filter) or a maximum (
for the low-pass filter) or a maximum (![]() for the high-pass filter), respectively.
for the high-pass filter), respectively.
You can see that the cut-off frequency actually is a remarkable point for a filter circuit.
Low-pass filter
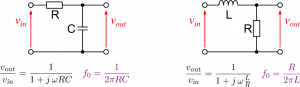
High-pass filter