Über Filter und Grenzfrequenzen

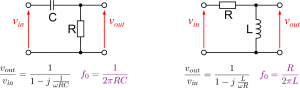
Gestern im Studentenpraktikum im Kurs Elektronik I kam eine gute Frage auf: Was macht eigentlich die Grenzfrequenz eines Filters so besonders? Warum suchen wir ausgerechnet nach einem Punkt, der oder einen Faktor unter der Amplitude das Passbandes liegt? Warum nicht , , ?

Die erste Antwort, die auch historische Bezüge in sich trägt, besteht darin, sich einen festen Widerstand und ein Signal mit einer Amplitude und ein weiteres Signal mit einer Amplitude anzusehen, und die umgesetzte elektrische Leistung zu berechnen:

Die Leistung ist also auf die Hälfte gesunken. Diese Leistung kann z.B. die elektrische Leistung sein, die in einem Lautsprecher in akustische Leistung umgesetzt wird, oder in einer Antenne in elektromagnetische Wellen.

Schon hier sollten wir aber notieren:

Aber war das schon alles? Es erscheint immer noch ziemlich willkürlich, ausgerechnet diesen Punkt zu betrachten. Schauen wir uns unsere einfachen RC-Filter an, so gibt es einen weiteren Anlass, gerade diese Frequenz besonders auszuzeichnen: In einem Tiefpassfilter haben wir eine konstante Amplitude für tiefe Frequenzen, während die Amplitude für hohe Frequenzen mit per Frequensdekade abnimmt. Zeichnen wir diese beiden Asymptoten in ein Bodediagramm ein, so schneiden sich die beiden Linien in genau einem Punkt – ja, genau, an der Grenzfrequenz (das Entsprechende gilt natürlich auch für ein Hochpassfilter). Wir können das deutlich sehen, wenn wir das entsprechende Gebiet des Bodediagramms vergrößern:

Bodediagramm eines Tiefpassfilters – Vergrößerung der Umgebung der Grenzfrequenz.

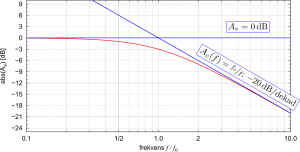
War das jetzt alles? Ist da noch mehr, was mit der Grenzfrequenz zu tun hat?

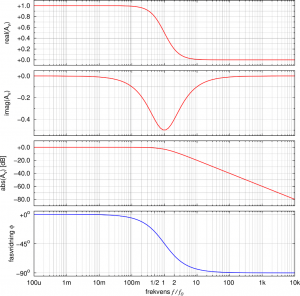
Wie wir schon wissen, so liegt die Phasenverschiebung zwischen Eingangs- und Ausgangssignal an der Grenzfrequenz bei (Hochpass) bzw. (Tiefpass). In der komplexen Schreibweise der -Methode bedeutet dies nicht anderes, als daß der Real- und der Imaginärteil der Überführungsfunktion hier denselben Absolutwert besitzen. Die genauen Verhältninsse zwischen Real- und Imaginärteil, Amplitude und Phasenwinkel habe ich weiter unten für Tief- und Hochpassfilter dargestellt.

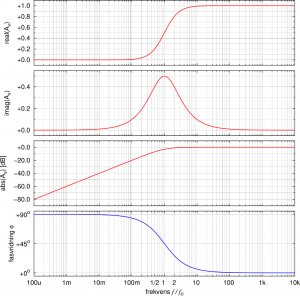
Ein interessantes Detail, das man hier sehen kann ist, daß der Imaginärteil der Überführungsfunktion an der Grenzfrequenz ein Minimum ( für das Tiefpassfilter) bzw. ein Maximum ( für das Hochpassfilter) aufweist.

Ihr seht, daß die Grenzfrequenz eine wichtige Bedeutung für ein Filter hat.

Tiefpassfilter

Tiefpassfilter: RC und RL.

Hochpassfilter

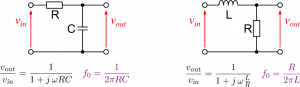
Hochpassfilter: RC und RL.